2018年普通高等学校招生全国(Ⅱ)统一考试
理科数学
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知集合![]() ,则
,则![]() 中元素的个数为
中元素的个数为
A.9B.8C.5D.4
3.函数![]() 的图像大致为
的图像大致为
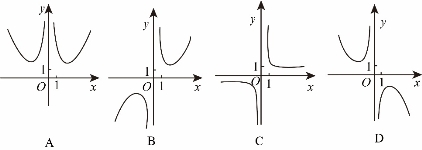
4.已知向量![]() ,
,![]() 满足
满足![]() ,
,![]() ,则
,则![]()
A.4B.3C.2D.0
 5.双曲线
5.双曲线![]() 的离心率为
的离心率为![]() ,则其渐近线方程为
,则其渐近线方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
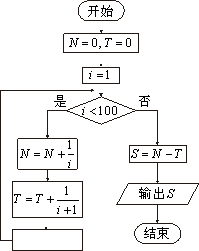
7.为计算![]() ,设计了右侧的程序框图,则在空白框中应填入
,设计了右侧的程序框图,则在空白框中应填入
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如![]() .在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在长方体![]() 中,
中,![]() ,
,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若![]() 在
在![]() 是减函数,则
是减函数,则![]() 的最大值是
的最大值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知![]() 是定义域为
是定义域为![]() 的奇函数,满足
的奇函数,满足![]() .若
.若![]() ,则
,则![]()
A.![]() B.0C.2D.50
B.0C.2D.50
12.已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 是
是![]() 的左顶点,点
的左顶点,点![]() 在过
在过![]() 且斜率为
且斜率为![]() 的直线上,
的直线上,![]() 为等腰三角形,
为等腰三角形,![]() ,则
,则![]() 的离心率为
的离心率为
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本题共4小题,每小题5分,共20分.
13.曲线![]() 在点
在点![]() 处的切线方程为__________.
处的切线方程为__________.
14.若![]() 满足约束条件
满足约束条件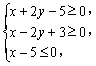 则
则![]() 的最大值为__________.
的最大值为__________.
15.已知![]() ,
,![]() ,则
,则![]() __________.
__________.
16.已知圆锥的顶点为![]() ,母线
,母线![]() ,
,![]() 所成角的余弦值为
所成角的余弦值为![]() ,
,![]() 与圆锥底面所成角为45°,若
与圆锥底面所成角为45°,若![]() 的面积为
的面积为![]() ,则该圆锥的侧面积为__________.
,则该圆锥的侧面积为__________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题,考生根据要求作答.
(一)必考题:共60分。
17.(12分)
记![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,已知
项和,已知![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() ,并求
,并求![]() 的最小值.
的最小值.
18.(12分)
下图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.
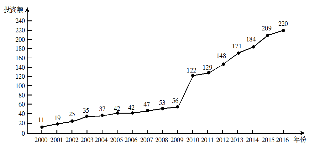 为了预测该地区2018年的环境基础设施投资额,建立了
为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
19.(12分)
设抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() .
.
(1)求![]() 的方程
的方程
(2)求过点![]() ,
,![]() 且与
且与![]() 的准线相切的圆的方程.
的准线相切的圆的方程.
20.(12分)
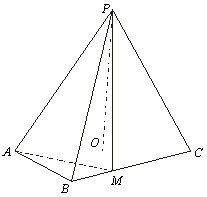
如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上,且二面角
上,且二面角![]() 为
为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
21.(12分)
已知函数![]() .
.
(1)若![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(2)若![]() 在
在![]() 只有一个零点,求
只有一个零点,求![]() .
.
(二)选考题:共10分.请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为
![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
23.[选修4-5:不等式选讲](10分)
设函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.






