2019中考数学一轮复习单元检测试卷
第十九单元 一次函数
考试时间:120分钟;满分:150分
学校:___________姓名:___________班级:___________考号:___________
得 分 | 评卷人 |
|
一、选择题(本大题共10小题,每小题4分,共40分)
1.在函数y=![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≤﹣3B.x≥﹣3C.x<﹣3D.x>﹣3
2.变量x与y之间的关系是y=2x﹣3,当因变量y=6时,自变量x的值是( )
A.9B.15C.4.5D.1.5
3.早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.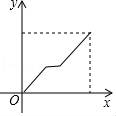 B.
B.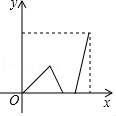
C.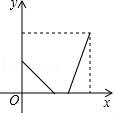 D.
D.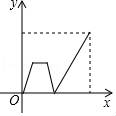
4.已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣x上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3B.y1<y2<y3C.y3>y1>y2D.y3<y1<y2
5.若函数y=kx(k≠0)的值随自变量的增大而增大,则函数y=x+2k的图象大致是( )
A.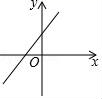 B.
B.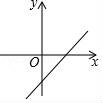
C.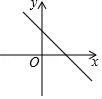 D.
D.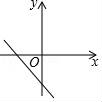
6.如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(6,4),若直线经过定点(1,0),且将平行四边形OABC分割成面积相等的两部分,则直线的表达式( )
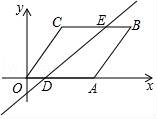
A.y=3x﹣2B.y=![]() x﹣
x﹣![]() C.y=x﹣1D.y=3x﹣3
C.y=x﹣1D.y=3x﹣3
7.如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程kx+b=0的解为x=2;②关于x的方程kx+b=3的解为x=0;③当x>2时,y<0;④当x<0时,y<3.其中正确的是( )
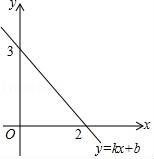
A.①②③B.①③④C.②③④D.①②④
8.速度分别为100km/h和akm/h(0<a<100)的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离y(km)与行驶时间t(h)之间的函数关系如图所示.下列说法:①a=60;②b=2;③c=b+![]() ;④若s=60,则b=
;④若s=60,则b=![]() .其中说法正确的是( )
.其中说法正确的是( )
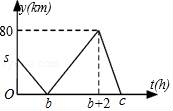
A.①②③B.②③④C.①②④D.①③④
9.如图,已知直线l:![]() ,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为( )
,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为( )
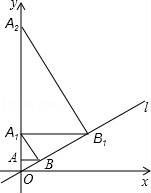
A.(0,128)B.(0,256)C.(0,512)D.(0,1024)
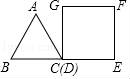
10.如图,等边三角形和正方形的边长均为a,点B,C,D,E在同一直线上,点C与点D重合.△ABC以每秒1个单位长度的速度沿BE向右匀速运动.当点C与点E重合时停止运动.设△ABC的运动时间为t秒,△ABC与正方形DEFG重叠部分的面积为S,则下列图象中,能表示S与t的函数关系的图象大致是( )
A.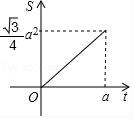 B.
B.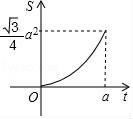
C. D.
D.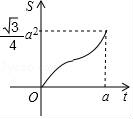
得 分 | 评卷人 |
|
二、填空题(本大题共4小题,每小题5分,共20分)
11.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时) | 0 | 1 | 2 | 3 |
y(升) | 100 | 92 | 84 | 76 |
由表格中y与t的关系可知,当汽车行驶小时,油箱的余油量为0.
12.若点(a,3)在函数y=2x﹣3的图象上,a的值是.
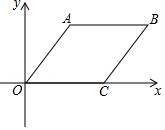
13.如图,O是坐标原点,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,则∠AOC的角平分线所在直线的函数关系式为.
14.点A(m,n)为直线y=﹣x+4上一动点,且满足﹣4<m<4,将O点绕点B(﹣![]() ,﹣
,﹣![]() )逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是.
)逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是.
得 分 | 评卷人 |
|
三、解答题(本大题共9小题,满分90分,其中第15,16,17,18题每题8分,19,20题每题10分,21,22题每题12分,23题14分)
15.已知y与x+2成正比,当x=4时,y=4.
(1)求y与x之间的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
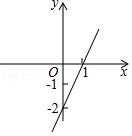
16.已知一次函数y=kx+b的图象如图所示
(1)求k、b的值;
(2)在平面直角坐标系内画出函数y=bx+k的图象;
(3)利用(2)中你所画的图象,写出0<x<1时,y的取值范围.
17.已知正比例函数y=kx图象经过点(3,﹣6),求:
(1)这个函数的解析式;
(2)判断点A(4,﹣2)是否在这个函数图象上;
(3)图象上两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
18.如图,在平面直角坐标系中,A(4,0),B(0,2),C(4,4).已知四边形ABCD为菱形,其中AB与BC为一组邻边.
(1)请在图中作出菱形ABCD,并求出菱形ABCD的面积;
(2)过点A的直线l:y=![]() x+b与线段CD相交于点E,请在图中作出直线l的图象,并求出△ADE的面积.
x+b与线段CD相交于点E,请在图中作出直线l的图象,并求出△ADE的面积.
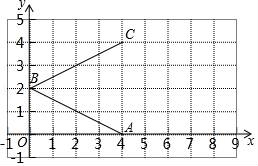
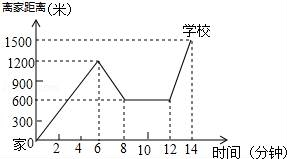
19.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是米.
(2)小明在书店停留了分钟.
(3)本次上学途中,小明一共行驶了米.一共用了分钟.
(4)我们认为骑单车的速度超过300米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的汽车速度最快,速度在安全限度内吗?
20.如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)y轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
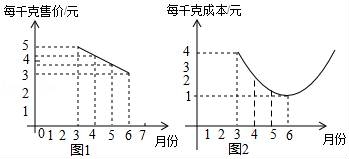
21.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每干克的收益是多少元?(收益=售价﹣成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
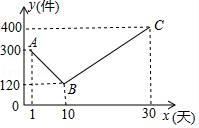
22.某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为w(元),求w与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元(不用说理)
23.阅读下列两段材料,回答问题:
材料一:点A(x1,y1),B(x2,y2)的中点坐标为(![]() ,
,![]() ).例如,点(1,5),(3,﹣1)的中点坐标为(
).例如,点(1,5),(3,﹣1)的中点坐标为(![]() ,
,![]() ),即(2,2).
),即(2,2).
材料二:如图1,正比例函数l1:y=k1x和l2:y=k2x的图象相互垂直,分别在l1和l2上取点A,B,使得AO=BO.分别过点A,B作x轴的垂线,垂足分别为点C,D.显然,△AOC≌△OBD.设OC=BD=a,AC=OD=b,则A(﹣a,b),B(b,a).于是k1=﹣![]() ,k2=
,k2=![]() ,所以k1•k2的值为一个常数.一般地,一次函数y=k1x+b1,y=k2x+b2可分别由正比例函数l1,l2平移得到.
,所以k1•k2的值为一个常数.一般地,一次函数y=k1x+b1,y=k2x+b2可分别由正比例函数l1,l2平移得到.
所以,我们经过探索得到的结论是:任意两个一次函数y=k1x+b1,y=k2x+b2的图象相互垂直,则k1•k2的值为一个常数.
(1)在材料二中,k1•k2=(写出这个常数具体的值);
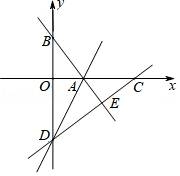
(2)如图2,在矩形OBAC中A(4,2),点D是OA中点,用两段材料的结论,求点D的坐标和OA的垂直平分线l的解析式;
(3)若点C′与点C关于OA对称,用两段材料的结论,求点C′的坐标.