2019中考数学一轮复习单元检测试卷

第十二单元 全等三角形

考试时间：120分钟；满分：150分

学校:___________姓名：___________班级：___________考号：___________

一、选择题（本大题共10小题，每小题4分，共40分）

1．下列图形是全等图形的是（　　）

A．B．

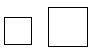C．D．

2．如图，点F，C在BE上，△ABC≌△DEF，AB和DE，AC和DF是对应边，AC，DF交于点M，则∠AMF等于（　　）

A．2∠BB．2∠ACBC．∠A+∠DD．∠B+∠ACB

第2题第3题第4题第5题

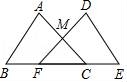
3．如图，已知∠1＝∠2，添加下列某条件，未必能判定△ABC≌BAD的是（　　）

A．AC＝BDB．AD＝BCC．∠l＝∠2D．∠C＝∠D

4．如图，△ABC中，AD⊥BC，D为BC的中点，以下结论：

（1）△ABD≌△ACD；（2）AB＝AC；（3）∠B＝∠C；（4）AD是△ABC的一条角平分线．

其中正确的有（　　）

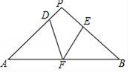
5．如图，在△PAB中，PA＝PB，D、E、F分别是边PA，PB，AB上的点，且AD＝BF，BE＝AF，若∠DFE＝34°，则∠P的度数为（　　）

A．112°B．120°C．146°D．150°

6．已知AD是△ABC的边BC上的中线，AB＝12，AC＝8，则边BC及中线AD的取值范围分别是（　　）

A．4＜BC＜20，2＜AD＜10B．4＜BC＜20，4＜AD＜20

C．2＜BC＜10，2＜AD＜10D．2＜BC＜10，4＜AD＜20

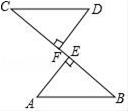
7．如图，AB＝CD，AE⊥BC，DF⊥BC，垂足分别为E，F，CE＝BF，下列结论错误的是（　　）

A．∠C＝∠BB．DF∥AEC．∠A+∠D＝90°D．CF＝BE

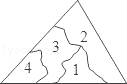
8．小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带（　　）去．

A．第1块B．第2块C．第3块D．第4块

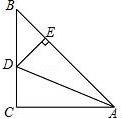
第7题第8题第9题第10题

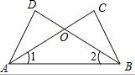
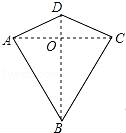
9．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD＝CD，AB＝CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积＝AC•BD，其中正确的结论有（　　）

A．①②B．①③C．②③D．①②③

10．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB于点E，则下列结论：①AD平分∠CDE；②∠BAC＝∠BDE；③DE平分∠ADB；④若AC＝4BE，则S△ABC＝8S△BDE．其中正确的有（　　）

A．1个B．2个C．3个D．4个

二、填空题（本大题共4小题，每小题5分，共20分）

11．如图，在△ABC中，AB＝3，AC＝2，BC边上的中线AD的长是整数，则AD＝．

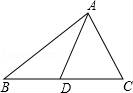
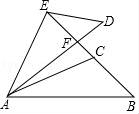
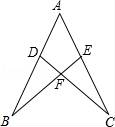
第11题 第12题 第13题 第14题

12．如图，△ABC≌△ADE，线段BC的延长线过点E，与线段AD交于点F，∠ACB＝∠AED＝108°，∠CAD＝12°，∠B＝48°，则∠DEF的度数．

13．如图，AB＝AC，要说明△ADC≌△AEB，添加的条件可以是（填写序号即可）

①∠B＝∠C②DC＝BE③AD＝AE④∠ADC＝∠AEB

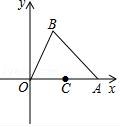
14．在平面直角坐标系中，点A、B、C的坐标分别为A（8，0），B（2，6），C（4，0），点P，Q是△ABO边上的两个动点（点P不与点C重合），以P，O，Q为顶点的三角形与△COQ全等，则满足条件的点P的坐标为．

三、解答题（本大题共9小题，满分90分,其中第15,16,17,18题每题8分，19,20题每题10分，21,22题每题12分，23题14分）

15．如图，△ACE≌△DBF，AC＝6，BC＝4．

（1）求证：AE∥DF；

（2）求AD的长度．

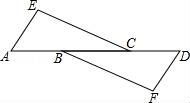
16．如图，已知AB∥CF，D是AB上一点，DF交AC于点E，若AB＝BD+CF，求证：△ADE≌△CFE．

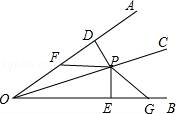
17．已知：如图，P是OC上一点，PD⊥OA于D，PE⊥OB于E，F、G分别是OA、OB上的点，且PF＝PG，DF＝EG．

求证：OC是∠AOB的平分线．

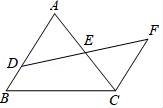
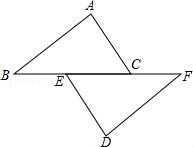
18．如图，已知点B，E，C，F在一条直线上，BE＝CF，AC∥DE，∠A＝∠D．

（1）求证：△ABC≌△DFE；

（2）若BF＝14，EC＝4，求BC的长．

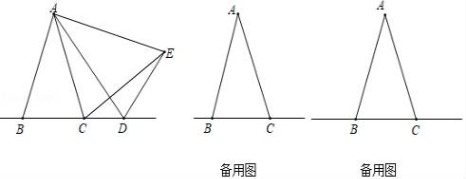
19．在△ABC中，AB＝AC，D是直线BC上一点，以AD为一条边在AD的右侧作△ADE，使AE＝AD，∠DAE＝∠BAC，连接CE．

（1）如图，当点D在BC延长线上移动时，若∠BAC＝25°，则∠DCE＝．

（2）设∠BAC＝α，∠DCE＝β．

①当点D在BC延长线上移动时，α与β之间有什么数量关系？请说明理由；

②当点D在直线BC上（不与B，C两点重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．

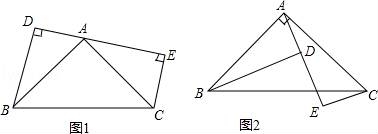
20．如图1，点A是线段DE上一点，∠BAC＝90°，AB＝AC，BD⊥DE，CE⊥DE，

（1）求证：DE＝BD+CE．

（2）如果是如图2这个图形，BD、CE、DE有什么数量关系？并证明．

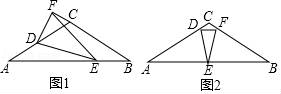
21．在△ABC中，D为BC上一点，连接AD，过点B作BE垂直于CA的延长线于点E，BE与DA的延长线相交于点F．

（1）如图1，若AB平分∠CBE，∠ADB＝30°，AE＝3，AC＝7，求CD的长；

（2）如图2，若AB＝AC，∠ADB＝45°，求证；BC＝DF．

22．在△ABC中，AC＝BC，D，E，F分别是直线AC，AB，BC上的点，且AD＝BE，AE＝BF．

（1）如图1，若∠DEF＝30°，求∠ACB的度数；

（2）设∠ACB＝x°，∠DEF＝y°，∠AED＝z°．

①求y与x之间的数量关系；

②如图2，E为AB的中点，求y与z之间的数量关系；

③如图2，E为AB的中点，若DF与AB之间的距离为8，AC＝16，求△ABC的面积．

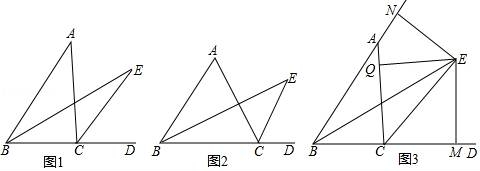
23．如图，在△ABC中，∠ABC的平分线BE与∠ACB外角的平分线CE交于点E．

（1）如图1，若∠BAC＝40°，求∠BEC的度数；

（2）如图2，将∠BAC变为60°，则∠BEC＝°．并直接写出∠BAC与∠BEC的关系；

（3）在图1的基础上过点E分别作EN⊥BA于N，EQ⊥AC于Q，EM⊥BD于M，如图3，求证：△ANE≌AQE，并直接写出∠NAE的度数．