2019中考数学一轮复习单元检测试卷
第四单元 几何图形初步
考试时间:120分钟;满分:150分
学校:___________姓名:___________班级:___________考号:___________
得 分 | 评卷人 |
|
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列几何体中,是圆锥的为( )
A.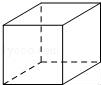 B.
B.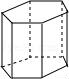 C.
C.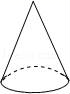 D.
D.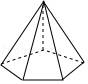
2.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆D.点、角、线段、长方体
3.用如图的图形,旋转一周所形成的图形是右边的( )
![]()
A.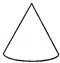 B.
B.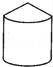 C.
C.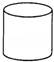 D.
D.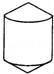
4.下列说法错误的是( )
A.两点之间线段最短B.两点确定一条直线
C.作射线OB=3厘米D.延长线段AB到点C,使得BC=AB
5.木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为( )
A.两点之间,线段最短
B.两点确定一条直线
C.过一点,有无数条直线
D.连接两点之间的线段叫做两点间的距离
6.如图,C是线段AB上的一点,点D是线段BC的中点,若AB=10,AC=6,则AD等于( )
![]()
A.4B.6C.7.5D.8
7.若∠α与∠β互余,且∠α:∠β=3:2,那么∠α的度数是( )
A.54°B.36°C.72°D.60°
8.如图,将三角板绕点O逆时针旋转一定角度,过点O在三角板MON的内部作射线OC,使得OC恰好是∠MOB的角平分线,此时∠AOM与∠NOC满足的数量关系是( )

A.∠AOM=∠NOCB.∠AOM=2∠NOCC.∠AOM=3∠NOCD.不确定
9.将一副直角三角尺按如图放置,若∠AOD=20°,则∠BOC的大小是( )
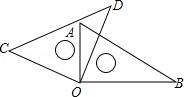
A.110°B.120°C.140°D.160°
10.如图,将长方形纸片进行折叠,ED,EF为折痕,A与A′、B与B′、C与C′重合,若∠AED=25°,则∠BEF的度数为( )
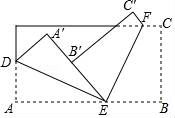
A.75°B.65°C.55°D.50°
得 分 | 评卷人 |
|
二、填空题(本大题共4小题,每小题5分,共20分)
11.把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=![]() ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为cm.
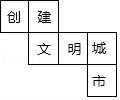
12.如图,这是一个正方体的展开图,则原正方体中与“创“字所在的面相对的面上标的字是.
13.如图,AB=24,点C为AB的中点,点D在线段AC上,且AD:DC=1:2,则DB的长度为.
![]()
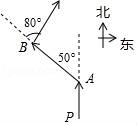
14.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为.
得 分 | 评卷人 |
|
三、解答题(本大题共9小题,满分90分,其中第15,16,17,18题每题8分,19,20题每题10分,21,22题每题12分,23题14分)
15.如图,B,C两点把线段AD分成2:3:4三部分,M,N分别是AD,AB的中点,CD=8cm,求MN的长.
![]()
16.如图在直角三角形ABC中,边AC长4cm,边BC长3cm,边AB长5cm.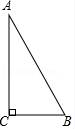
(1)三角形绕着边AC旋转一周,所得几何体的体积和绕着边BC旋转一周所得几何体体积是否一样?通过计算说明;
(2)若绕着边AB旋转一周,所得的几何体的体积是多少?
17.如图,OD、OC、OB、OA分别表示东西南北四个方向,OM的方向是西偏北50°,OE的方向是北偏东15°,OE是∠MOG的平分线,∠MOH=∠NOH=90°.
(1)OH的方向是,ON的方向是;(2)通过计算,判断出OG的方向;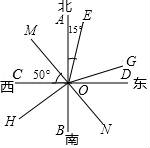
(3)求∠HOG的度数.
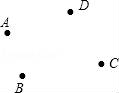
18.平面上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小(A,B,C,D四个村庄的地理位置如图所示),你能说明理由吗?
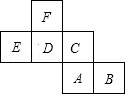
19.如图是一个正方体的展开图,标注了字母A,C的面分别是正方体的正面和底面,其他面分别用字母B,D,E,F表示.已知A=kx+1,B=3x﹣2,C=1,D=x﹣1,E=2x﹣1,F=x.
(1)如果正方体的左面与右面所标注字母代表的代数式的值相等,求出x的值;
(2)如果正面字母A代表的代数式与对面字母代表的代数式的值相等,且x为整数,求整数k的值.
20.阅读下列材料并填空:
(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?
我们知道,两点确定一条直线.平面上有2个点时,可以画![]() =1条直线,平面内有3个点时,一共可以画
=1条直线,平面内有3个点时,一共可以画![]() =3条直线,平面上有4个点时,一共可以画
=3条直线,平面上有4个点时,一共可以画![]() =6条直线,平面内有5个点时,一共可以画条直线,…平面内有n个点时,一共可以画条直线.
=6条直线,平面内有5个点时,一共可以画条直线,…平面内有n个点时,一共可以画条直线.
(2)运用:某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?
21.“三等分任意角”是数学史上一个著名问题,经过无数人探索,现在已经确信,仅用圆规直尺是不可能做出的.在探索过程中,我们发现,可以利用一些特殊的图形,把一个任意角三等分.如图:在∠MAN的边上任取一点B,过点B作BC⊥AN于点C,并作BC的垂线BF,连接AF,E是AF上一点,当AB=BE=EF时,有∠FAN=![]() ∠MAN,请你证明.
∠MAN,请你证明.
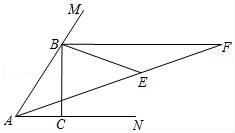
22.CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BECF;EF|BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<90°,且满足∠α+∠BCA=180°,请证明图中①的两个结论是否成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想:(不要求证明).
23.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
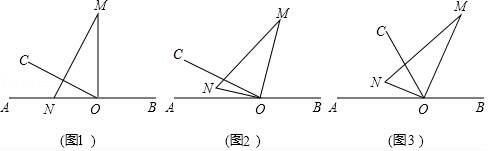
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.
①求t值;
②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点0顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.






