2019中考数学一轮复习单元检测试卷
第十七单元 勾股定理
考试时间:120分钟;满分:150分
学校:___________姓名:___________班级:___________考号:___________
得 分 | 评卷人 |
|
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列各组数中,是勾股数的是( )
A.1、2、3B.3、4、5C.12、15、18D.1、![]() 、3
、3
2.如果3,a,5是勾股数,则a的值是( )
A.4B.![]() C.4或
C.4或![]() D.4或34
D.4或34
3.如图,在正方形网格中,每个正方形的边长为1,则在△ABC中,边长为无理数的边数是( )
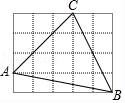
A.0B.1C.2D.3
4.在△ABC中,∠B=90°,若BC=3,AC=5,则AB等于( )
A.2B.3C.4D.![]()
5.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为( )
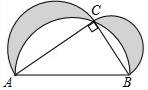
A.4B.4πC.8πD.8
6.如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
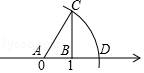
A.2.2B.![]() C.
C.![]() D.
D.![]()
7.我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是( )
A.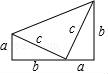 B.
B.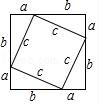
C.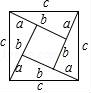 D.
D.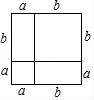
8.已知△ABC的三边为a,b,c,下列条件能判定△ABC为直角三角形的是( )
A.a:b:c=1:1:![]() B.a:b:c=1:1:
B.a:b:c=1:1:![]()
C.a:b:c=2:2:3D.a:b:c=![]() :2:
:2:![]()
9.“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
A.3B.5C.4.2D.4
10.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”.设这个人的身高是5尺,秋千的绳索始终拉的很直,则绳索长为( )
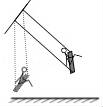
A.12.5尺B.13.5尺C.14.5尺D.15.5尺
得 分 | 评卷人 |
|
二、填空题(本大题共4小题,每小题5分,共20分)
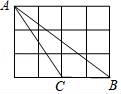
11.如图,长方形网格中每个小正方形的边长是1,△ABC是格点三角形(顶点都在格点上),则点C到AB的距离为.
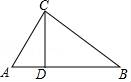
12.若CD是△ABC的高,AB=10,AC=6,BC=8,则CD的长为.
13.有两根木棒,分别长6cm、5cm,要再在7cm的木棒上取一段,用这三根木棒为边做成直角三角形,这第三根木棒要取的长度是.
14.勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面规律,第5个勾股数组为.

得 分 | 评卷人 |
|
三、解答题(本大题共9小题,满分90分,其中第15,16,17,18题每题8分,19,20题每题10分,21,22题每题12分,23题14分)
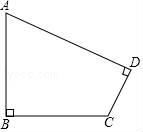
15.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的长.
16.某广场内有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=6m,BC=8m,CD=26m,AD=24m.求四边形ABCD空地的面积.
17.如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
(1)在网格中画出长为![]() 的线段AB.
的线段AB.
(2)在网格中画出一个腰长为![]() 、面积为3的等腰△DEF.
、面积为3的等腰△DEF.
18.如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
(1)如图△ABC中,AB=AC=![]() ,BC=2,求证:△ABC是“美丽三角形”;
,BC=2,求证:△ABC是“美丽三角形”;
(2)在Rt△ABC中,∠C=90°,AC=2![]() ,若△ABC是“美丽三角形”,求BC的长.
,若△ABC是“美丽三角形”,求BC的长.
19.在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.

20.如果a,b,c为正整数,且满足a2+b2=c2,那么,a、b、c叫做一组勾股数.
(1)请你根据勾股数的意思,说明3、4、5是一组勾股数;
(2)写出一组不同于3、4、5的勾股数;
(3)如果m表示大于1的整数,且a=4m,b=4m2﹣1,c=4m2+1,请你根据勾股数的定义,说明a、b、c为勾股数.
21.[问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
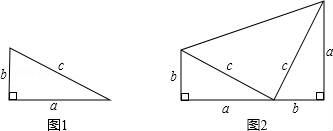
请你根据图1中的直角三角形,写出勾股定理内容;
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.
22.阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为﹣1,试求M、N两点的距离为;
(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.
(4)在(3)的条件下,平面直角坐标系中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标及PD+PF的最短长度.
23.如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
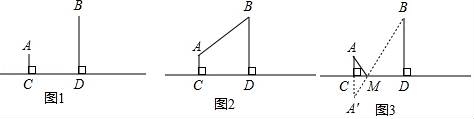
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选
方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)
方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?






