2019中考数学一轮复习单元检测试卷

第九单元 不等式与不等式组

考试时间：120分钟；满分：150分

学校:___________姓名：___________班级：___________考号：___________

一、选择题（本大题共10小题，每小题4分，共40分）

1．若m＜n，则下列不等式中一定成立的是（　　）

A．m﹣2＜n﹣2B．﹣m＜﹣nC．D．m2＜n2

2．若关于x的一元一次不等式组无解，则a的取值范围是（　　）

A．a≥1B．a＞1C．a≤﹣1D．a＜﹣1

3．不等式﹣2x+6＞0的解集在数轴上表示正确的是（　　）

A．B．

C．D．

4．某商品的进价是500元，标价为750元，商店要求以利润不低于5%的售价打折出售，此商品最低可以打（　　）

A．6折B．7折C．8折D．9折

5．解不等式的过程如下：

①去分母，得3x﹣2≤11x+7，

②移项，得3x﹣11x≤7+2，

③合并同类项，得﹣8x≤9，

④系数化为1，得．

其中造成错误的一步是（　　）

A．①B．②C．③D．④

6．不等式的负整数解有（　　）

A．1个B．2个C．3个D．4个

7．小明和同学约好周末去公园游玩，他从学校出发，全程2.1千米，此时距他和同学的见面时间还有18分钟，已知他每分钟走90米，途中发现自己可能迟到，于是改骑共享单车，速度为每分钟210米，如果小明不迟到，至少骑车多少分钟？设骑车x分钟，则列出的不等式为（　　）

A．210x+90（18﹣x）＜2.1B．210x+90（18﹣x）≥2100

C．210x+90（18﹣x）≤2100D．210x+90（18﹣x）≥2.1

8．不等式组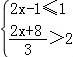的解集在数轴上表示正确的是（　　）

A．B．

C．D．

9．若不等式组的整数解共有三个，则a的取值范围是（　　）

A．5＜a＜6B．5≤a＜6C．5＜a≤6D．5≤a≤6

10．定义[x]为不超过x的最大整数，如[3.6]＝3，[0.6]＝0，[﹣3.6]＝﹣4．对于任意实数x，下列式子中错误的是（　　）

A．[x]＝x（x为整数）B．0≤x﹣[x]＜1

C．[x+y]≤[x]+[y]D．[n+x]＝n+[x]（n为整数）

二、填空题（本大题共4小题，每小题5分，共20分）

11．不等式的所有自然数解的和等于．

12．不等式组的解集为．

13．某公路维护站欲购置甲、乙两种型号清雪车共20台，甲型每台30万元，乙型每台15万元，若在购款不超过360万元，甲型、乙型都购买的情况下，甲型清雪车最多可购买台．

14．定义运算a⊗b＝a2﹣2ab，下面给出了关于这种运算的几个结论：

①2⊗5＝﹣16；

②是无理数；

③方程x⊗y＝0不是二元一次方程：

④不等式组的解集是﹣＜x＜﹣．

其中正确的是（填写所有正确结论的序号）

三、解答题（本大题共9小题，满分90分,其中第15,16,17,18题每题8分，19,20题每题10分，21,22题每题12分，23题14分）

15．解不等式：3﹣≥，并把解集在数轴上表示出来．

16．x取哪些非负整数时，的值大于与1的差．

17．解不等式组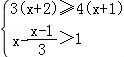：，并把解集在数轴上表示出来．

18．如图所示的是一个运算程序．

例如：根据所给的运算程序可知，当x＝5时，5×5+2＝27＜37，再把x＝27代入，得5×27+2＝137＞37，则输出的值为137．

（1）填空：当x＝10时，输出的值为；当x＝2时，输出的值为．

（2）若需要经过两次运算才能输出结果，求x的取值范围．

19．某城市平均每天处理垃圾700吨，有甲和乙两个处理厂处理，已知甲每小时可处理垃圾55吨，需要费用550元，乙厂每小时可处理垃圾45吨，需要费用495元．如果规定该城市每天用于处理垃圾的费用不得超过7370元，甲厂每天处理垃圾至少要多少吨？

20．某文化用品商店计划同时购进一批A、B两种型号的计算器，若购进A型计算器10只和B型计算器8只，共需要资金880元；若购进A型计算器2只和B型计算器5只，共需要资金380元．

（1）求A、B两种型号的计算器每只进价各是多少元？

（2）该经销商计划购进这两种型号的计算器共50只，而可用于购买这两种型号的计算器的资金不超过2520元．根据市场行情，销售一只A型计算器可获利10元，销售一只B型计算器可获利15元．该经销商希望销售完这两种型号的计算器，所获利润不少于620元．则该经销商有哪几种进货方案？

21．已知a＞0，符号[a]表示大于或等于a的最小正整数，如：[2，1]＝3，[4，8]＝5，[6]＝6，

（1）填空：[7]＝，若[a]＝4，则a的取值范围．

（2）某地运输公司规定出租车的收费标准是：3公里以内（包括3公里）收费5元；超出的部分，每公里加收2元（不足1公里按1公里计算）．现在y表示乘客应付的乘车费（单位：元），用a表示所行驶的路程（单位：公里），则乘车费可按如下的公式计算：

①当0＜a≤3时，y＝5；

②当a＞3时，y＝5+2×[a﹣3]．

某乘客乘车后付费15元，求该乘客所行驶的路程a（公里）的取值范围．

22．“保护好环境，拒绝冒黑烟”．某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．

（1）求购买A型和B型公交车每辆各需多少万元？

（2）预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型公交车x辆，完成下表：

（3）若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客量总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案的总费用最少？最少总费用是多少？

23．某公司为了更好治理污水质，改善环境，决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：

经调查：购买一台A型设备比购买一台B型设备多3万元，购买2台A型设备比购买3台B型设备少1万元．

（1）求a，b的值；

（2）经预算：市治污公司购买污水处理设备的资金不超过78万元，你认为该公司有哪几种购买方案；

（3）在（2）间的条件下，若每月要求处理的污水量不低于1620吨，为了节约资金，请你为该公司设计一种最省钱的购买方案．