2019-2020深圳市数学中考一模试题含答案

一、选择题

1．在“朗读者”节目的影响下，某中学开展了“好书伴我成长”读书活动．为了解5月份八年级300名学生读书情况，随机调查了八年级50名学生读书的册数，统计数据如下表所示：

关于这组数据，下列说法正确的是（　　）

A．中位数是2B．众数是17C．平均数是2D．方差是2

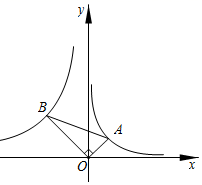
2．如图抛物线y＝ax2+bx+c的对称轴为直线x＝1，且过点（3，0），下列结论：①abc＞0；②a﹣b+c＜0；③2a+b＞0；④b2﹣4ac＞0；正确的有（　　）个．

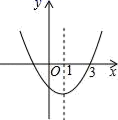
A．1B．2C．3D．4

3．如图的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿大半圆弧ACB路线爬行，乙虫沿小半圆弧ADA1、A1EA2、A2FA3、A3GB路线爬行，则下列结论正确的是( )

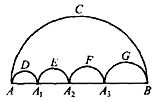
A．甲先到B点B．乙先到B点C．甲、乙同时到B点D．无法确定

4．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：

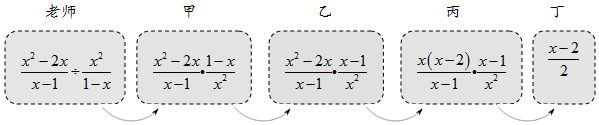
接力中，自己负责的一步出现错误的是（　　）

A．只有乙B．甲和丁C．乙和丙D．乙和丁

5．如图，AB是一垂直于水平面的建筑物，某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度（或坡比）为i=1：0.75、坡长为10米的斜坡CD到达点D，然后再沿水平方向向右行走40米到达点E（A，B，C，D，E均在同一平面内）．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°=0.45）（　　）

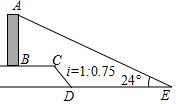
A．21.7米B．22.4米C．27.4米D．28.8米

6．不等式组的解集在数轴上表示正确的是（）

A．B．C．D．

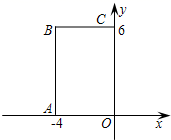
7．如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，

OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的，那么点B′的坐标是（）

A．（－2，3）B．（2，－3）C．（3，－2）或（－2，3）D．（－2，3）或（2，－3）

8．甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃~8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（）

A．1℃~3℃B．3℃~5℃C．5℃~8℃D．1℃~8℃

9．现定义一种变换：对于一个由有限个数组成的序列S0，将其中的每个数换成该数在S0中出现的次数，可得到一个新序列S1，例如序列S0：（4，2，3，4，2），通过变换可生成新序列S1：（2，2，1，2，2），若S0可以为任意序列，则下面的序列可作为S1的是（　　）

A．（1，2，1，2，2）B．（2，2，2，3，3）C．（1，1，2，2，3）D．（1，2，1，1，2）

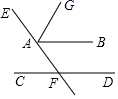
10．如图，直线，AG平分，，则的度数为

A．B．C．D．

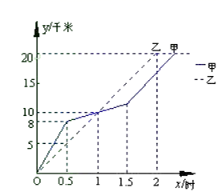
11．在全民健身环城越野赛中，甲乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米.其中正确的说法有（）

A．1个B．2个C．3个D．4个

12．如图，AB∥CD，∠C=80°，∠CAD=60°，则∠BAD的度数等于（　　）

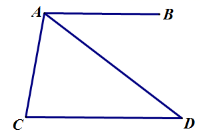
A．60°B．50°C．45°D．40°

二、填空题

13．如图，中，，顶点，分别在反比例函数与的图象上，则的值为_____．

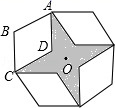
14．如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=2，则图中阴影部分的面积为．

15．如图，一张三角形纸片ABC，∠C=90°，AC=8cm，BC=6cm．现将纸片折叠：使点A与点B重合，那么折痕长等于cm．

16．已知反比例函数的图象经过点（m，6）和（﹣2，3），则m的值为________．

17．“复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车．“复兴号”的速度比原来列车的速度每小时快40千米，提速后从北京到上海运行时间缩短了30分钟，已知从北京到上海全程约1320千米，求“复兴号”的速度．设“复兴号”的速度为x千米/时，依题意，可列方程为_____．

18．等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是．

19．已知（a-4）（a-2）=3，则（a-4）2+（a-2）2的值为__________．

20．在学校组织的义务植树活动中，甲、乙两组各四名同学的植树棵数如下，甲组：9，9，11，10；乙组：9，8，9，10；分别从甲、乙两组中随机选取一名同学，则这两名同学的植树总棵数为19的概率______．

三、解答题

21．阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：，善于思考的小明进行了以下探索：

设（其中均为整数），则有．

∴．这样小明就找到了一种把部分的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

当均为正整数时，若，用含m、n的式子分别表示，得＝，＝；

（2）利用所探索的结论，找一组正整数，填空：＋＝(＋)2；

（3）若，且均为正整数，求的值．

22．“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A、B、C、D表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．

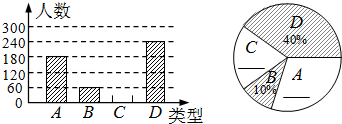
请根据以上信息回答：

（1）本次参加抽样调查的居民有多少人？

（2）将两幅不完整的图补充完整；

（3）若居民区有8000人，请估计爱吃D粽的人数；

（4）若有外型完全相同的A、B、C、D粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率．

23．已知：如图，点E，A，C在同一条直线上，AB∥CD，AB=CE，AC=CD．

求证：BC=ED．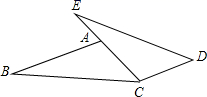

24．为了解某县建档立卡贫困户对精准扶贫政策落实的满意度，现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查（把调查结果分为四个等级：A级：非常满意；B级：满意；C级：基本满意；D级：不满意），并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题：

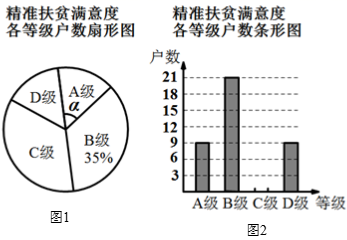
（1）本次抽样调查测试的建档立卡贫困户的总户数______.

（2）图1中，∠α的度数是______，并把图2条形统计图补充完整.

（3）某县建档立卡贫困户有10000户，如果全部参加这次满意度调查，请估计非常满意的人数约为多少户？

（4）调查人员想从5户建档立卡贫困户（分别记为）中随机选取两户，调查他们对精准扶贫政策落实的满意度，请用列表或画树状图的方法求出选中贫困户的概率.

25．小华想复习分式方程，由于印刷问题，有一个数“？”看不清楚：.

（1）她把这个数“？”猜成5，请你帮小华解这个分式方程；

（2）小华的妈妈说：“我看到标准答案是：方程的增根是，原分式方程无解”，请你求出原分式方程中“？”代表的数是多少？