2020年广东省深圳市罗湖区滨河中学中考数学一模试卷
一、选择题(共12小题;共36分)
1.(3分)下列各数中,是无理数的是( )
A.![]() B.
B.![]() C.
C.![]() D.3.1415
D.3.1415
2.(3分)以下给出的几何体中,主视图是矩形,俯视图是圆的是( )
A.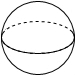 B.
B.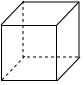
C.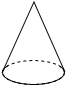 D.
D.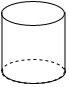
3.(3分)流感病毒的半径大约为0.00000045米,它的直径用科学记数法表示为( )
A.0.9×10﹣7B.9×10﹣6C.9×10﹣7D.9×10﹣8
4.(3分)改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
5.(3分)下列计算,正确的是( )
A.a2•a3=a6B.2a2﹣a=aC.a6÷a2=a3D.(a2)3=a6
6.(3分)不透明袋子中装有红、绿小球各一个,除颜色外无其余差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(3分)如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )
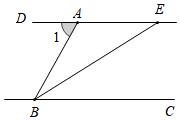
A.20°B.35°C.55°D.70°
8.(3分)若关于x的一元二次方程kx2﹣x﹣![]() =0有实数根,则实数k的取值范围是( )
=0有实数根,则实数k的取值范围是( )
A.k=0B.k≥﹣![]() C.k≥﹣
C.k≥﹣![]() 且k≠0D.k>﹣
且k≠0D.k>﹣![]()
9.(3分)下列命题是假命题的是( )
A.三角形的外心到三角形的三个顶点的距离相等
B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16
C.将一次函数y=3x﹣1的图象向上平移3个单位,所得直线不经过第四象限
D.若关于x的一元一次不等式组![]() 无解,则m的取值范围是m≤1
无解,则m的取值范围是m≤1
10.(3分)如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径画弧,分别交BA,BC于点M,N;再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.则下列说法中不正确的是( )
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.则下列说法中不正确的是( )
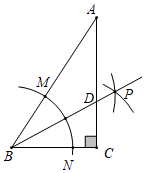
A.BP是∠ABC的平分线B.AD=BD
C.S△CBD:S△ABD=1:3D.CD=![]() BD
BD
11.(3分)如图,一艘船由A港沿北偏东65°方向航行30![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )km.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )km.
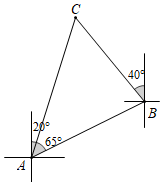
A.30+30![]() B.30+10
B.30+10![]() C.10+30
C.10+30![]() D.30
D.30![]()
12.(3分)如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连接MC,设FE与DC相交于点N.则4个结论:①DE=DF;②∠CME=∠CDE;③DG2=GN•GE;④若BF=2,则MC=![]() ;正确的结论有( )个
;正确的结论有( )个

A.4B.3C.2D.1
二、填空题(共4小题;共12分)
13.(3分)分解因式:a3+ab2﹣2a2b=.
14.(3分)若一组数据4,a,7,8,3的平均数是5,则这组数据的中位数是.
15.(3分)如图,在△ABC中,∠BAC的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F,若AB=8,AC=4,则CF的长为.
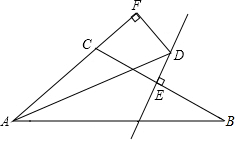
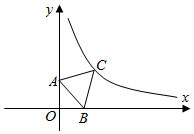
16.(3分)如图所示,△ABC为等边三角形,点A的坐标为(0,4),点B在x轴上,点C在反比例函数y=![]() 的图象上,则点B的坐标为.
的图象上,则点B的坐标为.
三、解答题(共7小题;共52分)3
17.(5分)计算:2sin60°+|![]() ﹣2|+(﹣1)﹣1﹣
﹣2|+(﹣1)﹣1﹣![]()
18.(6分)先化简,再求值:![]() ÷(a﹣
÷(a﹣![]() ),其中a=3,b=2﹣
),其中a=3,b=2﹣![]() .
.
19.(7分)“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
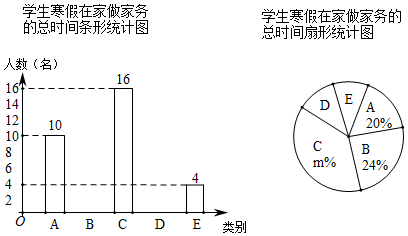
根据统计图提供的信息,解答下列问题:
(1)本次共调查了名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是,类别D所对应的扇形圆心角的度数是度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
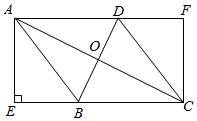
20.(8分)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF为矩形;
(2)连接OE,若AE=4,AD=5,求tan∠OEC的值.
21.(8分)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
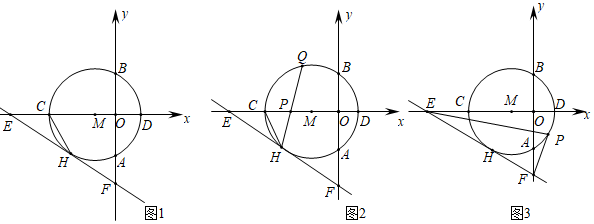
22.(8分)如图1所示,以点M(﹣1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E(﹣5,0),交y轴于点F(0,![]() ).
).
(1)求⊙M的半径r;
(2)如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC=![]() ,求
,求![]() 的值;
的值;
(3)如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+![]() PE的最小值.
PE的最小值.
23.(10分)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
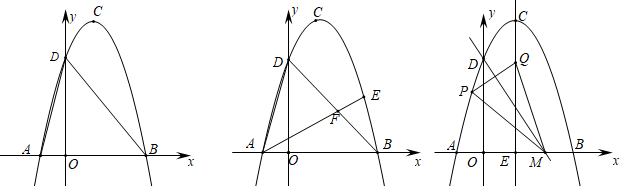
(1)求抛物线的解析式;
(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.
(3)如图3,点M的坐标为(![]() ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.






