深圳市 2020 年普通高中高三年级线上统一测试

数学（理科）

一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知集合A{0，1，2，3}，B{x|x22x30}，则A

2．设z23i，则z的虚部为

3．某工厂生产的30个零件编号为01，02，…，19，30，现利用如下随机数表从中抽取5个进行检

测.若从表中第1行第5列的数字开始，从左往右依次读取数字，则抽取的第5个零件编号为

A．25B．23C．12D.07

4．记Sn为等差数列{an}的前n项和，若a23，a59，则S6为

5．若双曲线xy（a0，b0）的一条渐近线经过点(1,2)，则该双曲线的离心率为

a2b21

6．已知tan3，则sin 2(π)

4

7．(x2)7的展开式中x3的系数为

x

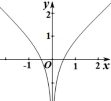
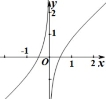
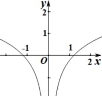
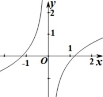
8．函数fxln | e2x1|x的图像大致为

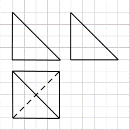
9．如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球表面积为

10．已知动点

（第9题图）

在以F，F为焦点的椭圆x2y上，动点N在以为圆心，半径长为|MF|

M1241M1

的圆上，则|NF2|的最大值为

11．著名数学家欧拉提出了如下定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半．此直线被称为三角形的欧拉线，该定理则被称为欧拉线定理．设点O，H分别是△ABC的外心、垂心，且M为BC中点，则

12．已知定义在[0π]上的函数f(x)sin(xπ)(0)的最大值为，则正实数的取值个数

，

463

最多为

二、填空题：本大题共4小题，每小题 5 分，共20分．

x2y20

13．若x,y满足约束条件xy10，则zx2y的最小值为        ．

x1

14．设数列{an}的前n项和为Sn，若Sn2ann，则a6．

15．很多网站利用验证码来防止恶意登录，以提升网络安全.某马拉松赛事报名网站的登录验证码由0，1，2，…，9中的四个数字随机组成，将从左往右数字依次增大的验证码称为“递增型

验证码”(如0123)，已知某人收到了一个“递增型验证码”，则该验证码的首位数字是1的概率为．

16．已知点M(m,m1)和点N(n,n1)(mn)，若线段MN上的任意一点P都满足：经过点P的

22

所有直线中恰好有两条直线与曲线C:y1x2x(1x3)相切，则|mn|的最大值为．

2

三 、 解答题： 共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考Th都必须作答．第22、23题为选考题，考Th根据要求作答．

(一 ) 必考题：共60分．

17．（本小题满分12分）

已知△ABC的内角A，B，C的对边分别为a，b，c，△ABC的面积为S，a2+b2c22S.

（1）求cosC；

（2）若acosBbsinAc，a，求b.

18．（本小题满分12分）

如图，在直四棱柱ABCDA1B1C1D1中，底面ABCD是平行四边形， 点M，N分别在棱C1C，

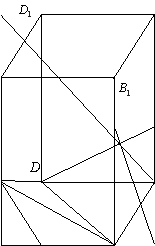
A1A上，且C1M2MC，A1N2NA.

1

（1）求证：NC1//平面BMD；

（2）若AA3，AB2AD2，DABπ，A1

13

求二面角NBDM的正弦值.M

NC

AB

（第18题图）

19．（本小题满分12分）

已知以F为焦点的抛物线C:y22px(p0)过点P(1,2)，直线l与C交于A，B两点，M为

AB中点，且OMOPOF.

（1）当3时，求点M的坐标；

（2）当OAOB12时，求直线l的方程.

20．（本小题满分12分）

在传染病学中，通常把从致病刺激物侵入机体或者对机体发生作用起，到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息，得到如下表格：

（1）   求这1000名患者的潜伏期的样本平均数x（同一组中的数据用该组区间的中点值作代表）；

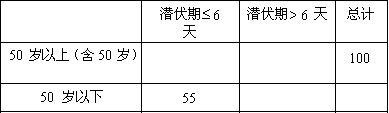
（2）该传染病的潜伏期受诸多因素的影响，为研究潜伏期与患者年龄的关系，以潜伏期是否超过6天为标准进行分层抽样，从上述1000名患者中抽取200人，得到如下列联表.请将列联表补充完整，并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关；

（3）以这1000名患者的潜伏期超过6天的频率，代替该地区1名患者潜伏期超过6天发生的概

率，每名患者的潜伏期是否超过6天相互独立.为了深入研究，该研究团队随机调查了20名患者，

其中潜伏期超过6天的人数最．有．可．能．（即．概．率．最．大．）是多少？ 附：

n(adbc)2

K，其中nabcd.

(ab)(cd)(ac)(bd)

21．（本小题满分12分）

已知函数f(x)exaln(x1).（其中常数e=2.718 28，是自然对数的底数）

（1）若aR，求函数f(x)的极值点个数；

（2）若函数f(x)在区间(1,1+ea)上不单调，证明：11

a.

aa1

（二）选考题：共10分．请考Th在第22、23两题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一题计分．

22．（本小题满分10分）选修4－4：坐标系与参数方程

x2

在直角坐标系xOy中，直线C的参数方程为

tcos,

（t为参数，为倾斜角），

1ytsin,

以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为4 sin．

（1）求C2的直角坐标方程；

（2）直线C1与C2相交于E,F两个不同的点，点P的极坐标为(23,π)，若

2EFPEPF，

求直线C1的普通方程．

23．（本小题满分10分）选修4－5：不等式选讲

已知a,b,c为正数，且满足abc1.

（1）9；

abc

证明：

（2）acbcababc8.

27