初中数学三角形、四边形、圆辅助线的添加方

01

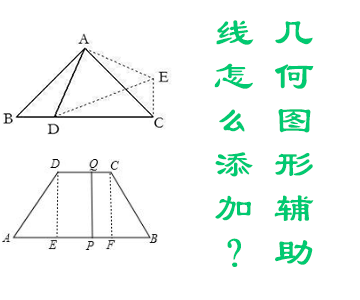
三角形中常见辅助线的添加

1. 与角平分线有关的

（1）可向两边作垂线；

（2）可作平行线，构造等腰三角形；

（3）在角的两边截取相等的线段，构造全等三角形。

2. 与线段长度相关的

（1）截长：

证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取一段，使得它和其中的一条相等，再利用全等或相似证明余下的等于另一条线段即可；

（2）补短：

证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延长一段，使得延长的部分等于另外一条较短的线段，再利用全等或相似证明延长后的线段等于那一条长线段即可；

（3）倍长中线：

题目中如果出现了三角形的中线，方法是将中线延长一倍，再将端点连结，便可得到全等三角形；

（4）遇到中点，考虑中位线或等腰等边中的三线合一。

3. 与等腰等边三角形相关的

（1）考虑三线合一；

（2）旋转一定的度数，构造全都三角形，等腰一般旋转顶角的度数，等边旋转60°。

02

四边形中常见辅助线的添加

1. 和平行四边形有关的辅助线作法

平行四边形是最常见的特殊四边形之一，它有许多可以利用性质，为了利用这些性质往往需要添加辅助线构造平行四边形。

（1）利用一组对边平行且相等构造平行四边形；

（2）利用两组对边平行构造平行四边形；

（3）利用对角线互相平分构造平行四边形。

2. 与矩形有关的辅助线作法

（1）计算型题，一般通过作辅助线构造直角三角形借助勾股定理解决问题。

（2）证明或探索题，一般连结矩形的对角线借助对角线相等这一性质解决问题。和矩形有关的试题的辅助线的作法较少。

3. 和菱形有关的辅助线的作法

和菱形有关的辅助线的作法主要是连接菱形的对角线，借助菱形的判定定理或性质定定理解决问题。

（1）作菱形的高；

（2）连结菱形的对角线。

4. 与正方形有关辅助线的作法

正方形是一种完美的几何图形，它既是轴对称图形，又是中心对称图形，有关正方形的试题较多。解决正方形的问题有时需要作辅助线，作正方形对角线是解决正方形问题的常用辅助线。

5. 与梯形有关的辅助线的作法

和梯形有关的辅助线的作法是较多的 ，主要涉及以下几种类型：

（1）作一腰的平行线构造平行四边形和特殊三角形；

（2）作梯形的高，构造矩形和直角三角形；

（3）作一对角线的平行线，构造直角三角形和平行四边形；

（4）延长两腰构成三角形；

（5）作两腰的平行线等。

03

圆中常见辅助线的添加

1. 遇到弦时（解决有关弦的问题时）

常常添加弦心距，或者作垂直于弦的半径（或直径）或再连结过弦的端点的半径。

作用：

① 利用垂径定理；

② 利用圆心角及其所对的弧、弦和弦心距之间的关系；

③ 利用弦的一半、弦心距和半径组成直角三角形，根据勾股定理求有关量。

2. 遇到有直径时

常常添加（画）直径所对的圆周角

作用：利用圆周角的性质得到直角或直角三角形

3. 遇到90度的圆周角时

常常连结两条弦没有公共点的另一端点

作用：利用圆周角的性质，可得到直径

4. 遇到弦时

常常连结圆心和弦的两个端点，构成等腰三角形，还可连结圆周上一点和弦的两个端点。

作用：

①可得等腰三角形；

②据圆周角的性质可得相等的圆周角。

5. 遇到有切线时

常常添加过切点的半径（连结圆心和切点）；

作用：利用切线的性质定理可得OA⊥AB，得到直角或直角三角形。

常常添加连结圆上一点和切点；

作用：可构成弦切角，从而利用弦切角定理。

6. 遇到证明某一直线是圆的切线时

（1） 若直线和圆的公共点还未确定，则常过圆心作直线的垂线段。

作用：若OA=r，则l为切线。

（2） 若直线过圆上的某一点，则连结这点和圆心（即作半径）

作用：只需证OA⊥l，则l为切线。

（3） 有遇到圆上或圆外一点作圆的切线。

7. 遇到两相交切线时（切线长）

常常连结切点和圆心、连结圆心和圆外的一点、连结两切点。

作用：据切线长及其它性质，可得到

① 角、线段的等量关系

② 垂直关系

③ 全等、相似三角形

8. 遇到三角形的内切圆时

连结内心到各三角形顶点，或过内心作三角形各边的垂线段。

作用：利用内心的性质，可得

① 内心到三角形三个顶点的连线是三角形的角平分线；

② 内心到三角形三条边的距离相等。

9. 遇到三角形的外接圆时

连结外心和各顶点

作用：外心到三角形各顶点的距离相等。

10. 遇到两圆外离时

（解决有关两圆的外、内公切线的问题）常常作出过切点的半径、连心线、平移公切线，或平移连心线。

作用：

①利用切线的性质；

②利用解直角三角形的有关知识。

11. 遇到两圆相交时

常常作公共弦、两圆连心线、连结交点和圆心等。

作用：

①利用连心线的性质、解直角三角形有关知识；

② 利用圆内接四边形的性质；

③ 利用两圆公共的圆周的性质；

④ 垂径定理。

12. 遇到两圆相切时

常常作连心线、公切线。

作用：

①利用连心线性质；

②切线性质等。

13. 遇到三个圆两两外切时

常常作每两个圆的连心线；

作用：可利用连心线性质。

14. 遇到四边形对角互补时

常常添加辅助圆。

作用：以便利用圆的性质。

来源：高昇教育