2020年广东省深圳实验学校中学部中考数学三模试卷
一、选择题(每题3分,共36分)
1.(3分)﹣![]() 的相反数是( )
的相反数是( )
A.2B.﹣2C.![]() D.﹣
D.﹣![]()
2.(3分)下列运算正确的是( )
A.3a+4b=7abB.(ab3)3=ab4
C.(a+2)2=a2+4D.x12÷x6=x6
3.(3分)下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.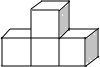 B.
B.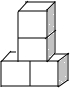
C.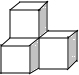 D.
D.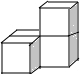
4.(3分)某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:
人数(人) | 1 | 3 | 4 | 1 |
分数(分) | 80 | 85 | 90 | 95 |
那么这9名学生所得分数的众数和中位数分别是( )
A.90,90B.90,85C.90,87.5D.85,85
5.(3分)如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BOD=70°,则∠CON的度数为( )

A.35°B.45°C.55°D.65°
6.(3分)如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )
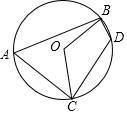
A.50°B.60°C.45°D.90°
7.(3分)已知4<m<5,则关于x的不等式组![]() 的整数解共有( )
的整数解共有( )
A.1个B.2个C.3个D.4个
8.(3分)关于x的一元二次方程(m﹣1)x2﹣2x﹣1=0有两个实数根,则实数m的取值范围是( )
A.m≥0B.m>0C.m≥0且m≠1D.m>0且m≠1
9.(3分)下列说法:
①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有( )个.
A.4B.3C.2D.1
10.(3分)一次函数y=ax+b与反比例函数y=![]() ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
A.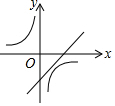 B.
B.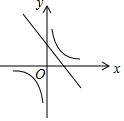
C.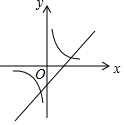 D.
D.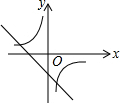
11.(3分)如图,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD:AB=3:1,则点C的坐标是( )
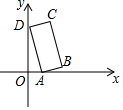
A.(2,7)B.(3,7)C.(3,8)D.(4,8)
12.(3分)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<0;④b2+8a>4ac,其中正确的有( )
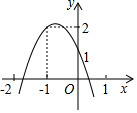
A.1个B.2个C.3个D.4个
二、填空题(每题3分,共12分)
13.(3分)中国首艘航母“辽宁号”满载排水量达67500吨.“67500”这个数据用科学记数法表示为.
14.(3分)因式分解:2a2﹣2=.
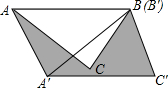
15.(3分)如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为.
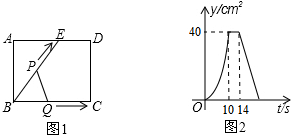
16.(3分)如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE﹣ED﹣DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.
给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③当14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
其中正确结论的序号是.
三、解答题(共52分)
17.(5分)计算:|﹣1+![]() |+4cos45°﹣(﹣
|+4cos45°﹣(﹣![]() )﹣2﹣
)﹣2﹣![]() •
•![]() +(π﹣3.14)0.
+(π﹣3.14)0.
18.(6分)先化简,再求值:![]() ,其中x的值从不等式组
,其中x的值从不等式组![]() 的整数解中选取.
的整数解中选取.
19.(7分)“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:
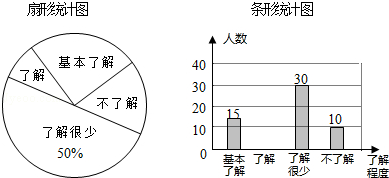
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
20.(8分)如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
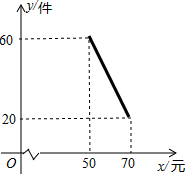
21.(8分)某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元.
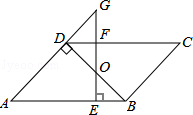
22.(9分)如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.
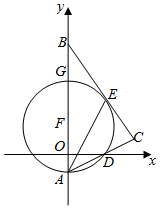
23.(9分)如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).