2020年广东省深圳市宝安区中考数学二模试卷
一、选择题(每题3分,共36分)
1.(3分)﹣5的倒数是( )
A.5B.﹣5C.![]() D.﹣
D.﹣![]()
2.(3分)我国于2019年10月1日在北京天安门广场举行大型阅兵仪式,在此次活动中,约有15000名官兵通过天安门广场接受党和人民的检阅,将数字15000用科学记数法表示为( )
A.1.5×103B.1.5×104C.0.15×105D.15×103
3.(3分)如图,由若干个棱长为1的小正方体摆成的几何体,则下列说法正确的是( )
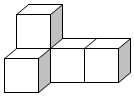
A.主视图的面积为4B.左视图的面积为4
C.俯视图的面积为3D.三种视图的面积都是4
4.(3分)下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B.
B.
C. D.
D.
5.(3分)下列运算正确的是( )
A.a2a3=a6B.2a+3a=5a2
C.(a+b)2=a2+b2D.(﹣ab2)3=﹣a3b6
6.(3分)某同学对一组数据2,3,4,5,5,7进行统计分析,误把3看成了8,则这组数据的计算结果不受影响的是( )
A.平均数B.中位数C.极差D.众数
7.(3分)下列命题中正确的是( )
A.1的平方根等于它本身
B.一元二次方程x2+x﹣1=0无解
C.任意多边形的外角和是360°
D.如果两个圆周角相等,那么它们所对的弧长一定相等
8.(3分)小天使童装店一件童装标价80元,在促销活动中,该件童装按标价的6折销售,仍可获利20%,则这种童装每件的进价为( )元.
A.30B.40C.50D.60
9.(3分)定义一种新运算:(x1,y1)(x2,y2)=x1x2+y1y2,如(2,5)(1,3)=2×1+5×3=17,若(1,x)(2,﹣5)=7,则x=( )
A.﹣1B.0C.1D.2
10.(3分)如图,抛物线y=ax2+bx+c(a≠0)的顶点为P(﹣1,0),则下列结论错误的是( )
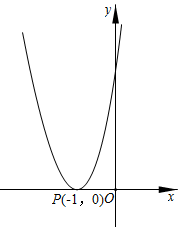
A.b>0
B.a=c
C.当x>0时,y随x的增大而增大
D.若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2
11.(3分)如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于M、N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC=( )
AB的长为半径作弧,两弧相交于M、N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC=( )
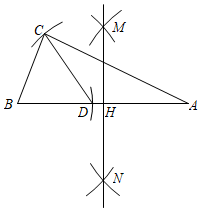
A.52°B.55°C.56°D.60°
12.(3分)如图,在△ABC中,∠ACB=90°,AC=BC,点D为边AC上一点,连接BD,作AH⊥BD的延长线于点H,过点C作CE∥AH与BD交于点E,连接AE并延长与BC交于点F,现有如下4个结论:①∠HAD=∠CBD;②△ADE∽△BFE;③CE•AH=HD•BE;④若D为AC中点,则![]() =(
=(![]() )2.其中正确结论有( )
)2.其中正确结论有( )
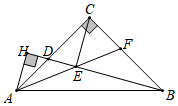
A.1个B.2个C.3个D.4个
二、填空题(每小题3分,共12分)
13.(3分)因式分解:x2y﹣4y=.
14.(3分)一个正方体的骰子六个面分别标有数字1、2、3、4、5、6,则扔一次骰子朝上的数字满足不等式x≤4的概率是.
15.(3分)如图,从甲楼顶部A处测得乙楼顶部D处的俯角α为30°,又从A处测得乙楼底部C处的俯角β为60°.已知两楼之间的距离BC为18米,则乙楼CD的高度为.(结果保留根号)
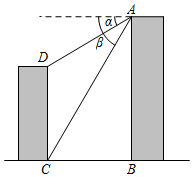
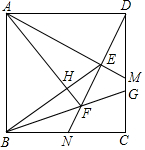
16.(3分)如图,在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,连接AM和DN交于点E,连接BE,作AH⊥BE于点H,延长AH与DN交于点F,连接BF并延长与CD交于点G,则MG的长度为.
三、解答题(本题共7小题,共52分)
17.(5分)计算:![]() .
.
18.(5分)先化简,再求值:![]() ,其中x=2.
,其中x=2.
19.(8分)面对突如其来的疫情,全国人民响应党和政府的号召,主动居家隔离.随之而来的,则是线上买菜需求激增.某小区为了解居民使用买菜APP的情况,通过制作无接触配送置物架,随机抽取了若干户居民进行调查(每户必选且只能选最常用的一个APP),现将调查结果绘制成如下两幅不完整的统计图:(A:天虹到家,B:叮咚买菜,C:每日优鲜,D:盒马鲜生)
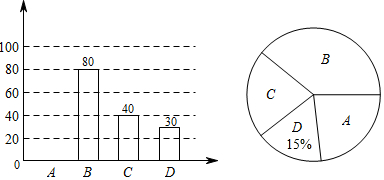
(1)本次随机调查了户居民;
(2)补全条形统计图的空缺部分;
(3)若该小区共有1200户居民,请估计该小区居民选择“C:每日优鲜”的大约有户;
(4)某日下午,张阿姨想购买苹果和生菜,各APP的供货情况如下:天虹到家仅有苹果在售,叮咚买菜仅有生菜在售,每日优鲜仅有生菜在售,盒马鲜生的苹果、生菜均已全部售完,则张阿姨随机选择两个不同的APP能买到苹果和生菜的概率是.
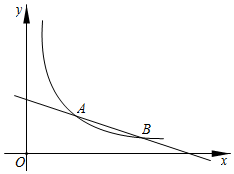
20.(7分)如图,一次函数y1=﹣![]() x+3与反比例函数y2=
x+3与反比例函数y2=![]() 的图象交于A、B两点,A点的横坐标为3.
的图象交于A、B两点,A点的横坐标为3.
(1)求反比例函数的解析式;
(2)结合图象,直接写出y1<y2时,x的取值范围.
21.(8分)在我市雨污分流工程中,甲、乙两个工程队共同承担茅洲河某段720米河道的清淤任务,已知甲队每天能完成的长度是乙队每天能完成长度的2倍,且甲工程队清理300米河道所用的时间比乙工程队清理200米河道所用的时间少5天.
(1)甲、乙两工程队每天各能完成多少米的清淤任务;
(2)若甲队每天清淤费用为2万元,乙队每天清淤费用为0.8万元,要使这次清淤的总费用不超过60万元,则至少应安排乙工程队清淤多少天?
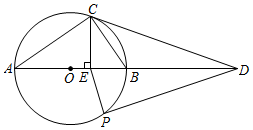
22.(9分)如图,AB是⊙O的直径,C为⊙O上一点,作CE⊥AB于点E,BE=2OE,延长AB至点D,使得BD=AB,P是弧AB(异于A,B)上一个动点,连接AC、PE.
(1)若AO=3,求AC的长度;
(2)求证:CD是⊙O的切线;
(3)点P在运动的过程中是否存在常数k,使得PE=k•PD,如果存在,求k的值,如果不存在,请说明理由.
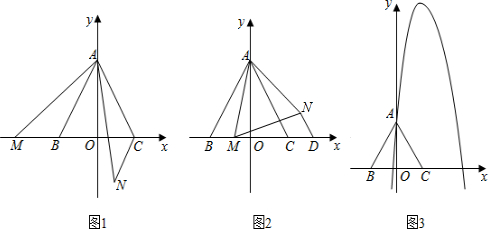
23.(10分)如图1,在平面直角坐标系中,等边△ABC的边BC在x轴上,A(0,3),B(﹣![]() ,0),点M(m,0)为x轴上的一个动点,连接AM,将AM绕点A逆时针旋转60°得到AN.
,0),点M(m,0)为x轴上的一个动点,连接AM,将AM绕点A逆时针旋转60°得到AN.
(1)当M点在B点的左方时,连接CN,求证:△BAM≌△CAN;
(2)如图2,当M点在边BC上时,过点N作ND∥AC交x轴于点D,连接MN,若S四边形ACDN=![]() S△MND,试求D点的坐标;
S△MND,试求D点的坐标;
(3)如图3,是否存在点M,使得点N恰好在抛物线y=﹣2x2+4![]() x+3上,如果存在,请求出m的值,如果不存在,请说明理由.
x+3上,如果存在,请求出m的值,如果不存在,请说明理由.