2019-2020学年广东省深圳市南山区第二外国语学校七年级（上）期中数学试卷

一、选择题（共12小题）

1．（3分）在﹣3，﹣1，0，1四个数中，比﹣2小的数是（　　）

A．﹣3B．﹣1C．0D．1

2．（3分）温家宝总理有句名言：多么小的问题乘以13亿，都会变得很大；多么大的经济总量，除以13亿都会变得很小．将1300000000用科学记数法表示为（　　）

A．13×108B．1.3×108C．1.3×109D．1.39

3．（3分）下列计算正确的是（　　）

A．﹣2a+5b＝3abB．﹣22+|﹣3|＝7C．3ab2﹣5b2a＝﹣2ab2D．+（）﹣1＝﹣1

4．（3分）如图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体“着”相对的面上的汉字是（　　）

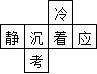
A．冷B．静C．应D．考

5．（3分）已知|a﹣2|+（b+3）2＝0，则ba的值是（　　）

A．﹣6B．6C．﹣9D．9

6．（3分）如果单项式2a2m﹣5bn+2与ab3n﹣2的和是单项式，那么m和n的取值分别为（　　）

A．2，3B．3，2C．﹣3，2D．3，﹣2

7．（3分）若a，b互为相反数，c，d互为倒数，则代数式（a+b﹣1）（cd+1）的值是（　　）

A．1B．0C．﹣1D．﹣2

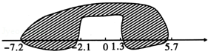
8．（3分）如图所示，有几滴墨水滴在数轴上，则被墨迹遮住的所有整数的和为（　　）

A．﹣11B．1C．﹣15D．﹣6

9．（3分）已知a﹣b＝3，c+d＝2，则（a+c）﹣（b﹣d）的值为（　　）

A．1B．﹣1C．5D．﹣5

10．（3分）下列说法，正确的有（　　）

（1）整数和分数统称为有理数；（2）任何有理数都有倒数；

（3）一个数的绝对值一定为正数；（4）立方等于本身的数是1和﹣1．

A．1个B．2个C．3个D．4个

11．（3分）若多项式ax2+2x﹣y2﹣7与x2﹣bx﹣3y2+1的差与x的取值无关，则a﹣b的值为（　　）

A．1B．﹣1C．3D．﹣3

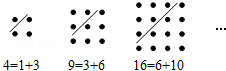
12．（3分）古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（　　）

A．13＝3+10B．25＝9+16

C．36＝15+21D．49＝18+31

二、填空题（共4小题）

13．（3分）如果风车顺时针旋转60°记作+60°，那么逆时针旋转25°记作．

14．（3分）如果对于任何非零有理数a，b定义一种新的运算“★”如下：a★b＝，则﹣4★2的值为．

15．（3分）若代数式4x2﹣2x+5的值是7，则代数式2x2﹣x+1的值是．

16．（3分）如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所填整数之和都相等，则第2013个格子中的整数是．

三、解答题（共7小题）

17．计算与化简：

（1）（2）

（3）（4）．

18．化简

（1）（﹣2ab+3a）﹣2（2a﹣b）+2ab；

（2）先化简，再求值：5a2+3b2+2（a2﹣b2）﹣（5a2﹣3b2），其中a＝﹣1，b＝．

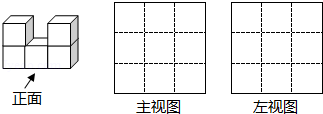
19．5个棱长为1的正方体组成如图的几何体．

（1）该几何体的体积是（立方单位），表面积是（平方单位）

（2）画出该几何体的主视图和左视图．

20．某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

（1）接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

（2）若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

（3）若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

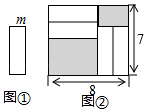
21．把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面长为8，宽为7的长方形盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示设图中小长方形的宽为m．

（1）小长方形的长为（用含m的代数式表示）；

（2）求图②中两块阴影部分周长的和．

22．观察下列等式，，，

将以上三个等式两边分别相加得：．

（1）猜想并写出：＝．

（2）直接写出下列各式的计算结果：

①＝；

②＝．

（3）探究并计算：．

23．结合数轴与绝对值的知识回答下列问题：

（1）数轴上表示4和1的两点之间的距离是；表示﹣3和2两点之间的距离是；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|．如果表示数a和﹣2的两点之间的距离是3，那么a＝；

（2）若数轴上表示数a的点位于﹣4与2之间，求|a+4|+|a﹣2|的值；

（3）当a取何值时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值是多少？请说明理由．